ARTICLE: The Formation of Massive Stars: Accretion, Disks, and the Development of Hypercompact H II Regions

Read the Paper by E. Keto (2002)

Summary by: Yucong Zhu

Abstract

The hypothesis that massive stars form by accretion can be investigated by simple analytical calculations that describe the effect that the formation of a massive star has on its own accretion flow. Within a simple accretion model that includes angular momentum, that of gas flow on ballistic trajectories around a star, the increasing ionization of a massive star growing by accretion produces a three-stage evolutionary sequence. The ionization first forms a small quasi-spherical H II region gravitationally trapped within the accretion flow. At this stage the flow of ionized gas is entirely inward. As the ionization increases, the H II region transitions to a bipolar morphology in which the inflow is replaced by outflow within a narrow range of angle aligned with the bipolar axis. At higher rates of ionization, the opening angle of the outflow region progressively increases. Eventually, in the third stage, the accretion is confined to a thin region about an equatorial disk. Throughout this early evolution, the H II region is of hypercompact to ultracompact size depending on the mass of the enclosed star or stars. These small H II regions whose dynamics are dominated by stellar gravitation and accretion are different than compact and larger H II regions whose dynamics are dominated by the thermal pressure of the ionized gas.

Great presentation by D. Muders about Spectral Line Observing

http://www.mpifr-bonn.mpg.de/div/effelsberg/SummerSchool/presentations/Muders-Spectral-Line-Observing.pdf

ARTICLE: Dust Grain-Size Distributions and Extinction in the Milky Way, Large Magellanic Cloud, and Small Magellanic Cloud

Read the paper by Weingartner & Draine (2001)

Summary by Max Moe and Katherine Rosenfeld.
Click here to download a pdf version of the class handout.

Abstract:

We construct size distributions for carbonaceous and silicate grain populations in different regimes for the Milky Way, LMC, and SMC. The size distributions include very small carbonaceous grains (including polycyclic aromatic hydrocarbon molecules) to account for the observed infrared and microwave emission from the diffuse interstellar medium. Our distributions reproduce the observed extinction of starlight, which varies depending on the interstellar environment through which the light travels. As shown by Cardelli, Clayton, and Mathias in 1989, these variations can be roughly parameterized by the ratio of visual extinction to reddening, . We adopt a fairly simple functional form for the size distributions, characterized by several parameters. We tabulate these parameters for various combinations of values for and , the Carbon abundance of very small grains. We also find size distributions for the line to HD 210121 and for sigh lines in the LMC and SMC. For several size distributions, we evaluate the albedo and scattering asymmetry parameter and present model extinction curves extending beyond the Lyman limit.

Background and Motivation:

The size of  dust grains along with  composition and geometry will determine the extinction of light as it travels through a dust cloud in the interstellar medium. The intensity goes as:

and so the extinction goes as:
.
The optical depth, , is related to to the size of the particles via their cross section. Previous to this work, other works (Mathis, Rumpl, & Nordsiek) had fit observed interstellar extinction using distributions of particle sizes well fit by a power law with index of about -3.5. Since that work in 1977, further observations of the diffuse interstellar medium suggested the existence of population of dust grains smaller than 50 angstroms. Furthermore, the lack of a 10 micron silicate feature suggested that this population should be largely composed of non-silicate grains and specific emission features were identified with carbonaceous compositions, specifically polycyclic aromatic hydrocarbons (PAHs). This paper tried to fit the extinctions that would result from a large small and large(er) grain population to reproduce the observed extinctions along various lines of sight.

 

Figure 4 from Mathis, Nordsieck, and Rumpl (1977) showing the modeled optical depth (dots and triangles) and observed optical depth (solid one). The dashed line is the contribution of graphite to the extinction.

Considering different lines of sight is important because extinction varies on the environment that the light is passing though. The ratio of extinction in the V band (e.g. visual extinction) to reddening, , had been previously shown to parametrize this extinction. Therefore the model featured in this paper used this parameter as a proxy of interstellar environment.

The Calculation

Grain size distribution:

Lacking a theory for the distribution of interstellar grain sizes, the authors used a simple functional form that had control over some maximum grain size, the steepness of this size cutoff, and the slope of the distribution of grains below the cutoff. They included two main species of grains, silicate and carbonaceous, where both had the same functional form but with an additional small grain population for the carbonaceous grains. They modeled this population using two log-normal size distributions centered at 3.5 and 30 to explain observed dust emission in the microwave and IR bands as well as the 750 and 2175 extinction features. See equations (2) – (6) to see the equations written out in full. Taking both grain species together leaves 11 parameters for fitting: 5 for silicon and 6 for cabonaceous grains. The extra parameter is the Carbon abundance, $b_c$, which is a proxy for the contribution of the small grains.

Modeling the extinction:

Given a grain-size distribution and its composition, the authors then calculate the extinction at a specific wavelength:

.

is the column density of grains with size less than a and is computed from the grain size distribution. The hard physics comes from teh extinction efficiency factor, which is generally a function of size, geometry, composition, and wavelength. The authors assume a simple spherical geometry and grains of a single composition – no ice mantles, mixed species, or conglomerated grains (see figure below). The calculation is done using a Mie scattering code that requires the dialectric function of the material (also a function of size, composition, and wavelength). The Mie scattering theory also considred albedo and asymmetry effects.

Albedo and asymmetry for a number of size distributions. Figure 15 from Weingartner and Draine.

For the silicate grains the authors use results from laboratory measurement of crystalline olivine smoothed over to remove a feature that is not observed. The carbonaceous grains are assumed to have a compositional distributiion as well where the smallest grains are PAH molecule, largest are graphite, and in between are some mixture. Since we don’t really know what the PAHs are exactly, the dialectric function is derived from astronomical observations.

Example extinction coefficients calculated from Mie Theory. From pg 58 of Voshchinnikov's "Optics of Cosmic Dust I"

Putting all of this together, the authors generate extinction curves for a given and and fit by minimizing one or two error functions. The first (case B) considers the error in the modeled and observed extinction. The other (case A) includes abundance and depletion values calculated from solar neighborhood values. The motivation for Case A is to avoid fits for high that reduce the grain volume past astrophysical intuition. Click here for a graphical sketch of the fitting process.

Grain-size distributions for Rv = 3.1. Figure 2 from Weingartner & Draine.

Model extinction curve optimized to fit the observed curve. Figure 8 from Weingartner & Draine.

Results and Discussion:

The paper considers dust in the Milky Way and towards HD 210121, the LMC and the SMC. With a small value of , features weaker than parametrized by , and a strong UV rise, HD 210121 was a test of the model. The authors were able to find grain-size distributions for and conclude that their grain model dealt well with thin line of sight. Table 2 contains the fitted parameters and the silicate grain volume for all cases exceeds that of the solar neighborhood. In class we discussed how this parameter probes star formation history since silicates are produced in supernovae and not in the winds of hot AGB stars like carbonaceous grains. Next they considered the lines of sight towards the metal poor LMC and SMC – a useful test of the model applied to extragalactic sources.

Direct or in situ measurement of ISM grain size distributions are rare and difficult to make. High altitude airplanes can collect inter-planetary dust (IPD) including GEMS grains (glass with embedded metal and sulfides) that, while much larger than the dust considered in this paper, are very primitive grains. NASA’s Stardust mission captured cometary particles and successfully delivered the payload back to Earth.

An interplanetary dust particle. From http://www.astro.washington.edu/users/brownlee/.

A GEMS particle. Image from http://stardust.jpl.nasa.gov.

The Ulysses and Galileo spacecraft also made in situ measurement of the local interstellar medium by measuring the impact of interstellar grains. The model presented in this paper appears to underestimate the number of large particles while overestimating the number of small particles (Frisch et al, 1999). Size-sorting and segregation are listed as possible causes of the disagreement.

 

Mass distribution of grains in the local ISM from spacecraft measurements and the presented models. Figure 24 from Weingartner & Draine.

While there are a number of acknowledged caveats assumptions in this relatively simple model, the model appears consistent with observations. Improvements that could be added to the model include adding a coating layer to the grains to reproduce the 3.4 micron feature or weak inter-stellar bands. Regardless, this simple model is sufficient and consistent in reproducing extinction curves so that errors and deviations in depletion, metallicities, dielectric constants, etc. are somewhat negligible. In addition, for a given environment the grain size distribution appears to vary. This suggests that small grains come together to form large grains especially in dense clouds. Similarly, collisions in shock waves can shatter the large grains and replenish the small grain population. Lastly, the cutoff in the size distribution is limited by the timescales of coagulation, shattering, accretion, and erosion along with the proportion between PAH molecules (small grains) and graphite (large grains).

One caveat is that while this paper assume spherical dust grains, real dust is more composite, fluffy, and amorphous. Furthermore, the derived grain-size distribution is disparate from dust in the local ISM. Interstellar dust passing through our solar system has a steeper slope dominated by larger grains as well as a larger cut-off in maximum size. Fundamentally, the dielectric functions used are not accurate for silicates and graphites, and especially so for PAHs. Lastly, degeneracies remain in some fitting parameters (e.g. the carbon grain-size slope at small sizes vs. ) so there parameters must be constrained from other observations.

For more information:

• Heidelberg Cosmic Dust Group
• Voshchinnikov’s Optics of Cosmic Dust I

The Cold ISM: (Atomic (21-cm), Molecular)

These online notes accompany the class discussion of the cold phase of the Interstellar Medium (ISM), discussed in AY201b class on (2/15/2010 , 2/17/2010, and 2/22/2010).

Additional Material:

• Radiative Processes of 21cm Formalism: Lengthy derivations of optical effects of 21cm radiation are attached as a PDF here. The ubiquity of equations demanded a different format than the wordpress post. For definitions of , etc, please reference Chapter 7 of Draine.
• Primary reference material is from Bruce Drain’s Physics of the Interstellar and Intergalactic Medium, Princeton University Press, Chapters 29 through 33. Figures are reproduced with permission of the author.
• This post will focus on the cold neutral phase of the interstellar medium. For more on the different phases of the ISM, check out Tanmoy’s post about the 1977 McKee and Ostriker paper.
• Molecular Cloud complexes log-plot sketch. Although the mass of the cloud complex does not exactly correlate with the inverse of number density, I hope this plot will visualize the differences between these different cloud types.

HI Clouds: Observations (Ch 29)

HI regions are primarily observed through the 21-cm (1420 MHz) line transition that results from the spin-flip of a neutral hydrogen atom from the triplet state to the singlet state. This transition was predicted to be visible by Van de Hulst in 1944, and was discovered by Ewen and Purcell in 1951, from the lab window of Harvard’s very own Jefferson Lab. If you’re interested, see the NRAO’s web page for more information about the historic achievement. Believe it or not, the actual horn antenna that made the detection now sits outside the offices at the NRAO Green Bank campus. Other teams of astronomers were very close to detecting the line, and once they learned of Ewen’s novel frequency-switching technique to reduce the noise, they were able to confirm the discovery of the 21-cm emission. For a really interesting discussion on why Ewen and Purcell succeeded, check out K. Stephan’s article in IEEE. Today, there is a quest for the analogous deuterium line at 327 MHz. For more on deuterated species, check out this posting on the arXiv by Bell et al 2011.

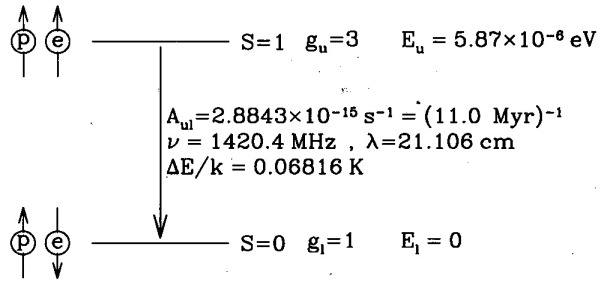
The hyperfine splitting of the 1s ground state of the hydrogen atom, resulting in 21cm radiation. (Fig 8.1 from Draine).

For an introductory quantum mechanical derivation of the 21-cm line (hyperfine splitting), please see section 6.5 of David Griffith’s Introduction to Quantum Mechanics. (See Figure 8.1 in Draine). The rate of spontaneous decay after being excited is on the order of one decay every 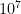years.

Approximately 60% (by mass) of gas in Milky Way is in HI regions, where hydrogen is atomic. This makes up about 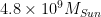, which is about 4.4% of the total visible matter. (The rest of the gas is 23% ionized hydrogen, and 17% molecular clouds) (Draine Table 1.2). HI is not really in clouds like molecular hydrogen (), and has a filling factor of 20% to 90% depending on the situation. The principle results from 21-cm line surveys can be found by Kulkami and Heiles 1998, in Galactic and Extragalactic Radio Astronomy, Verschur and Kellermann.

Consider the following important definitions relevant to HI 21-cm observations and modelling:

• Permitted Transition: These atomic and molecular transitions are what we generally think of when we work with the quantum mechanics of atoms and molecules. They occur relatively quickly and are the dominant transitions at high densities (such as the atmosphere of the earth). For example, H and H.
• Forbidden Transition: Many of the transitions that are governed by basic quantum mechanical selection rules are most relevant for conditions where there are collisions, or in the absence of external fields and spin-orbit coupling. Forbidden transitions are made possible through magnetic dipole or electric quadrupole transitions from atoms that are collisionally excited. As one might expect in the low density regions of the ISM, these transitions are very common (regardless of being termed “forbidden”). As Tanmoy’s comment explains, forbidden transitions generally take much longer to decay, and thus in higher density regions, the excited state is usually de-excited by a collision rather than emission of radiation.
• Critical Density: The density at which the collisions can keep up with the spontaneous radiative transitions. Defined as 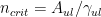, where means “upper-to-lower,” is the Einstein A-coefficient (units 1/s), and is the collisional rate coefficient (units 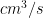). If 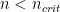, then the line flux is 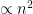, but if the then the line flux is , the column density.

Recall that the time constant years, thus for HI in the ISM 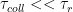. Which means that in the cold neutral medium (CNM) HI is primarily collisonally excited. However, the energy difference between the two spin states is small enough that the cosmic microwave radiation itself is strong enough to populate the upper spin state. Thus, the upper spin state contains approx 75% of the HI, and therefore HI emissitivity essentially independent of spin temperature. However, in the warm neutral medium (WNM), Ly 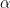can play a role (K&H and Field 1959).

The distribution of matter in the cold interstellar medium (ISM).

Radial Distribution of HI

Using radial velocity measurements, the spiral arms of our galaxy can be identified by the peaks of the 21cm line, since these are the regions where the intensity is strongest due to the abundance of HI.

Maps of HI in our galaxy: Fig 9 of Nakanishi and Sofue 2003.

The Zeeman effect introduces a frequency shift for left and right circularly polarized radiation. For regions with simple line profiles, this can be used to determine B field (parallel). The interstellar B field is on the order of 10 micro Gauss.

For more detailed information on excitation temperature, line profiles, and more, reference the 21cm radiation supplement and Draine Chapter 8. First year students can also reference their AY150 problem sets #3 and #7.

HI Clouds: Heating and Cooling (pg 337) (Ch 30)

The following processes are responsible for the heating and cooling of HI regions:

• Cosmic ray ionization
• photoionization by x-rays of H, He
• photoionization of dust grains by starlight UV
• photoionization of C, Mg, Si, Fe, etc by starlight UV
• Heating by shocks and magneto-hydrodynamics (MHD)

How cosmic rays interact with HI regions is largely dictated by the ionization state of the HI. A cosmic ray will ionize neutral hydrogen. The primary electron from this ionization can interact with the nearby HI in two ways. If the fractional ionization is high, then the electron has a high probability of scattering with other electrons via long-range Coulomb interactions, converting all of the initial kinetic energy into heat. If the fractional ionization is low, however, then the electron can then create a secondary ionization of another neutral hydrogen atom, or simply excite it’s electron into a higher energy level.

X-rays are an important source of heating only in clouds that are close to strong sources of < 200 eV x-rays. Lower energy x-rays can heat surface of an HI cloud, while higher energy x-rays can penetrate all the way down into the cloud (and possibly through it).

The photoelectric heating of dust is dominated by photons h nu > 8 eV. Photoelectrons (electrons emitted from dust grains via the photoelectric effect) are the dominant heating mechanism in the diffuse neutral ISM.

Line cooling is an important process where by atoms are collisionally excited, and then radiatively deexcited, releasing their radiation. Important lines such as [C II] 158 microns and [O I] 63 microns dominate the cooling for T < 10^4 K. (Include Figure 30.1, cooling rate graph). The critical densities for these lines are /, so collisional de-excitations of these lines in the diffuse ISM are unimportant.

Pressure Balance in HI regions

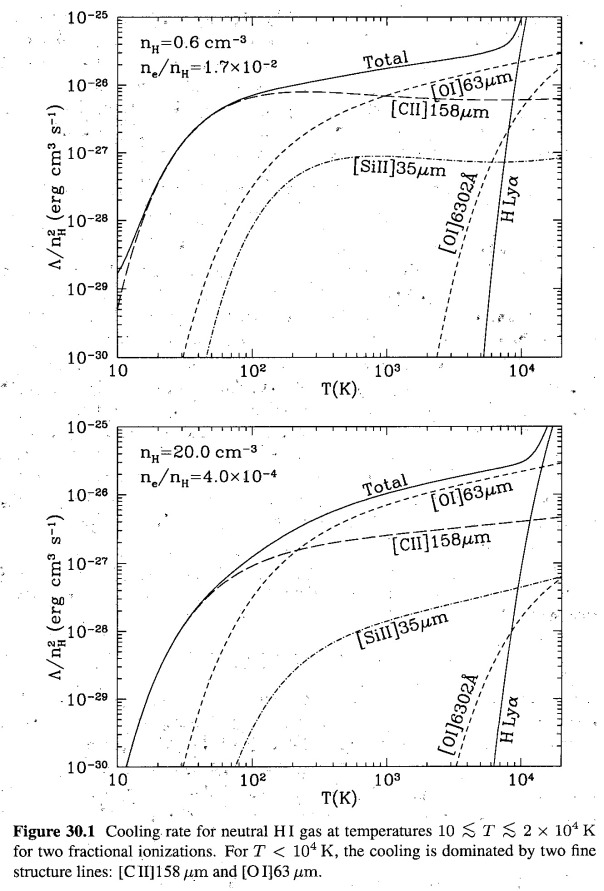
First, fix the pressure and then see where heating and cooling balance. For diffuse material, we have the warm neutral medium (WNM). For more compact material, we have the cold neutral medium (CNM).  The central points of these is unstable, and the ISM will separate out into two phases. This theory was first developed by Field (1969), but then photoelectric heating by dust was developed, and reworked (Figure 30.2 for net heating, cooling). Table 30.1 in Draine gives the conditions at stable equilibrium, the state of ionization and the emission spectrum.

Molecular Hydrogen (Ch 31)

For those unfamiliar with astro-jargon, astronomers have many colloquial names to refer to the many different ionization states of hydrogen. So far, we have referred to neutral, atomic hydrogen (one atom) as HI. If this single hydrogen atom is ionized (it lost it’s electron), it is termed HII.  However, if we have a diatomic molecule comprised of two hydrogen atoms, we follow the regular chemical convention and call this . Which means it is a nuisance to be precise when stating in conversation whether you are observing HII or .

The formation of is an interesting process. Because is a homogeneous diatomic molecule, it has no electric dipole moment, and thus there is no easy way (asymmetry of charge) to remove energy from the system via reactions like . in astrophysical situations is formed by radiative association and associative detachment. First, the ion is combined with neutral H, and then the extra electron is radiated away in this exothermic ion-molecule reaction. In the absence of dust, this is the dominant channel of formation.

However, dust can be used as a catalyst to expedite the formation of . Once a hydrogen atom hits a grain, it performs a random walk on surface, and settles down. After some time, another H might impact the (relatively) large surface area of the grain, random walk into the previous one, combine, and release enough energy to get kicked off the grain surface as an molecule. Alyssa likened termed this the “singles bar” scenario of formation.  This can also spin up the dust grain, giving rise to the continuum microwave emission.

The principal destruction process of is photodissociation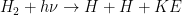

If a molecular cloud of or other species is of significant size, then it is likely it will be self-shielding. Photoexcitation transitions at the outer surface of the cloud become optically thick and the inside of the cloud is shielded from starlight from outside. These photoexcitations change vibrational and rotational levels by UV pumping. Later, the cascades back down via spontaneous emission by quadropole transitions, since there it has no electric dipole moment.

Vibrational levels have lifetimes ~10^6 s (~ a few weeks), and collisional dexcitation is unlikely at these densities. However, in the ground vibrational state, the lowest rotational levels last long enough that they can be collisionally deexcited.

Below is an interesting plot of the rotational excitation of in diffuse clouds for various column densities. If the self-shielding is low, then the rotation distribution (which rotational states does fill?) is insensitive to the gas temperature because it is the result of UV pumping. However, for larger column densities, the effect of self-shielding increases and the fraction of hydrogen in the upper rotational levels () decreases. For very high column densities, the UV pumping rates are small enough that the rotation temperature is an accurate measure of the gas temperature.

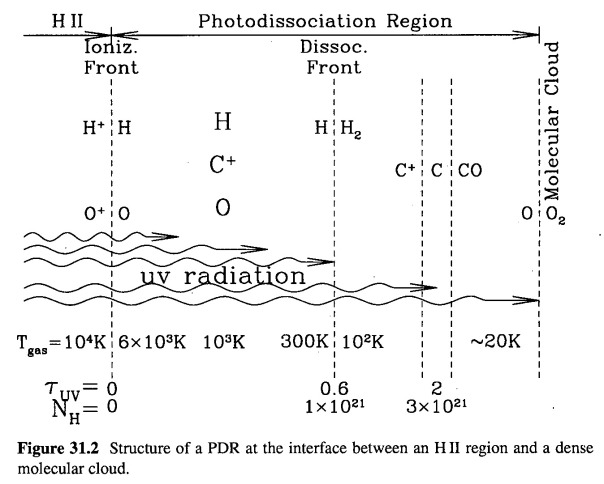
The interface between the HII region and the dense molecular cloud is called a Photodissociation Region (PDR), which bounded by an ionization front and a photodissociation front. We will hear more about this from student #5 on 2/24 and 3/1 (to be linked in the future).

Molecular Clouds: Observations (Ch 32)

Molecular clouds are separated based upon their optical appearance (diffuse, transulcent, or dark), which is really a measure of , the visual extinction.

Diffuse and transluscent clouds: pressure-confined, self-gravity. Large . There are even some infrared dark clouds.

There is some ambiguity between “clump” and “core” amongst authors. Giant Molecular cloud and dark clouds are distinguished by mass. Groups of clouds are cloud complexes, and structures within a cloud are called clumps. See Draine Table 32.2 for terminology for cloud complexes and components.

If the clumps are forming stars, then they are called star-forming clumps.

Cores are density spikes that will form a single or binary star. Most of the mass is in Giant Molecular Cores with .

Molecular clouds were originally discovered by star counts; astronomers such as Barnard concluded that the large patches of stars missing in the Milky Way were actually blocked by dust. Nowadays, these clouds are commonly observed through molecular line emission, and then use a conversion factor to get the abundance of .

Although the mass of the cloud complex does not exactly correlate with the inverse of number density, I made a rough log-plot sketch to visualize the differences between these different cloud types.

ARTICLE: Why are most molecular clouds gravitationally unbound?

Read the paper by C.L. Dobbs, A. Burkert, and J.E. Pringle (2011)

Summary by Elisabeth Newton

Abstract

The most recent observational evidence seems to indicate that giant molecular clouds are predominantly gravitationally unbound objects. In this paper we show that this is a natural consequence of a scenario in which cloud-cloud collisions and stellar feedback regulate the internal velocity dispersion of the gas, and so prevent global gravitational forces from becoming dominant. Thus, while the molecular gas is for the most part gravitationally unbound, local regions within the denser parts of the gas (within the clouds) do become bound and are able to form stars. We find that the observations, in terms of distributions of virial parameters and cloud structures, can be well modeled provided that the star formation efficiency in these bound regions is of order 5 – 10 percent. We also find that in this picture the constituent gas of individual molecular clouds changes over relatively short time scales, typically a few Myr.

Discussion of Assignment 1: Schematic of the Milky Way (Chris Beaumont’s version)

The list below is a fairly complete subsample of the questions asked during assignment one. I have arranged them into three categories, correlated with my own ignorance on various subjects. I speculate (or, in rare cases, know) that questions in the hardest group are open research issues. Questions in the second category are likely the kinds of questions a subject-area expert could answer. Questions in the last category are the most well-understood, and will likely be covered during this course. I have added commentary where I think I have something to add

ARTICLE: A theory of the interstellar medium – Three components regulated by supernova explosions in an inhomogeneous substrate

Read the paper by C.F. McKee & J.P. Ostriker (1977)

Summary by: Tanmoy Laskar

Abstract

Supernova explosions in a cloudy interstellar medium produce a three-component medium in which a large fraction of the volume is filled with hot, tenuous gas. In the disk of the galaxy the evolution of supernova remnants is altered by evaporation of cool clouds embedded in the hot medium. Radiative losses are enhanced by the resulting increase in density and by radiation from the conductive interfaces between clouds and hot gas. Mass balance (cloud evaporation rate = dense shell formation rate) and energy balance (supernova shock input = radiation loss) determine the density and temperature of the hot medium. A self-consistent model of the interstellar medium developed herein accounts for the observed pressure of interstellar clouds, the galactic soft X-ray background, the O VI absorption line observations, the ionization and heating of much of the interstellar medium, and the motions of the clouds.