ARTICLE: Interpreting Spectral Energy Distributions from Young Stellar Objects

Posted by: Meredith MacGregor

1. Introduction

When discussing young stellar objects and protoplanetary disks (as well as many other topics in astronomy), astronomers continually throw out the term ‘SED.  In early April, I attended a conference titled ‘Transformational Science with ALMA: From Dust to Rocks to Planets– Formation and Evolution of Planetary Systems.’  And, I can attest to the fact that the term ‘SED’ has come up in a very significant fraction of the contributed talks.  For those not intimately familiar with this sub-field, this rampant use of abbreviations can be confusing, making it difficult to glean any useful take-aways from a talk.  So, in addition to summarizing the article by Robitaille et al. (2007), the goal of this post is to give a bit of an introduction to the terminology and motivation for the growing field of star and planetary system formation.

SEDs: What They Are and Why We Care So Much

The abbreviation ‘SED’ stands for ‘Spectral Energy Distribution.’  If you want to sound like an expert, this should be pronounced exactly as it appears (analogous to the non-acronym ‘said’).  A SED is essentially a graph of flux versus wavelength.  In the context of the Robitaille et al. article, we are most interested in the SEDs for young stars and the envelopes and disks surrounding them.  So, why exactly does the flux from a young stellar object (YSO) vary with wavelength?  As it turns out, different regions of the YSO emit at different wavelengths.  This means that when we observe at different wavelengths, we are actually probing distinct regions of the star and its surrounding disk and envelope. By tracing out the entire SED for a YSO, we can determine what the geometry, structure, and constituents are for that object.

Before we go too far, it is worth taking a moment to clarify the terminology used to classify young stars.  A young stellar object or YSO is typically defined as any star in the earliest stages of development.  YSOs are almost always found in or near clouds of interstellar dust and gas.  The broad YSO class of objects is then divided into two sub-classes: protostars and pre-main sequence stars.  Protostars are heavily embedded in dust and gas and are thus invisible at optical wavelengths.  Astronomers typically use infrared, sub-millimeter, and millimeter telescopes to explore this stage of stellar evolution, where a star acquires the bulk of its material via infall and accretion of surrounding material.  Pre-main sequence (PMS) stars are defined to be low mass stars in the post-protostellar phase of evolution.  These stars have yet to enter the hydrogen-burning phase of their life and are sill surrounded by remnant accretion disks called ‘protoplanetary’ disks.  A more detailed a summary of this classification scheme can be found here.  However, because the evolution of young stars is far from well-understand, astronomers often typically these words interchangeably.

SEDs for pre-main sequence stars are often seen to have a bump or excess in the infrared. This bump is generally interpreted as being due to thermal emission from warm dust and gas surrounding the central star. As an illustrative example, let’s consider a protoplanetary disk around a young star. The image below is taken from a review article by Dullemond & Monnier (2010) and shows a graphical representation of the emission spectrum from such a disk.

A graphical representation of the emission spectrum from a protoplanetary disk and the telescopes that can be used to probe different regions of the disk. Taken from Dullemond & Monnier (2010).

In this case, emission in the near-infrared traces the warmer inner regions of the disk.  As you move into submillimeter wavelengths, you start to probe the outer, cooler regions of the disk.  By modeling the observed SED of a pre-main sequence star, you can determine what components of the source are contributing to the observed flux.  The second figure below is taken from a paper by Guarcello et al. (2010).  The left panel of this figure shows the observed SED (solid line) of a BWE star (in line with other ridiculous astronomy acronyms, this stands from ‘blue stars with excesses’) and the unreddened photospheric flux we would expect to see if the star did not have a disk (dashed line).  The right panel shows a model fit to this data.  The authors describe the observed SED using a model with four distinct components, each represented by a colored line in the figure: (1) emission from the reddened photosphere of the central star, (2) radiation scattered into the line of sight from dust grains in the disk, (3) emission from a collapsing outer envelope, and (4) thermal emission from a circumstellar disk.  The summation of these four component makes up the complete SED for this BWE star.

Left panel: The observed SED (solid line) of a BWE star and the unreddened photospheric flux we would expect to see if the star did not have a disk (dashed line). Right panel: A four component model fit to this data. Taken from Guarcello et al. (2010).

Describing and Classifying the Evolution of a Protostar

As a protostar evolves towards the Zero Age Main Sequence (ZAMS), the system geometry (and thus the SED) will evolve as well. Therefore, the stage of evolution of a protostar is often classified according to both the general shape and the features of the SED.  A graphical overview of the four stages of protostellar evolution are shown below (Andrea Isella’s thesis, 2006).  Class 0 objects are characterized by a very embedded central core in a much larger accreting envelope.  The mass of the central core grows in Class I objects and a flattened circumstellar accretion disk develops.  For Class II objects, the majority of circumstellar material is now found in a disk of gas and dust.  Finally, for Class III objects, the emission from the disk becomes negligible and the SED resembles a pure stellar photosphere.  The distinction between these different classes was initially defined by the slope of the SED (termed the ‘spectral index’) at infrared wavelengths.  Class I sources typically have SEDs that rise in the far- and mid-infrared, while Class II sources have flat or falling SEDs in the mid-infrared.  However, this quantitative distinction is not always clear and is not an effective way to unambiguously distinguish between the different object classes (Protostars and Planets V, page 127-128).

A graphical overview of the four stages of protostar evolution taken from Andrea Isella’s thesis (2006). A typical SED of each class is shown in the left column and a cartoon of the corresponding geometry is shown in the right column.

2. The Article Itself

One common method of fitting SEDs is to assume a given gas and circumstellar dust geometry and set of dust properties (grain size distribution, composition, and opacity), and then use radiative transfer models to predict the resulting SED and find a set of parameters that best reproduce the observations.  However, fitting SEDs by trial and error is a time consuming way to explore a large parameter space.  The problem is even worse if you want to consider thousands of sources.  So, what’s to be done?  Enter Robitaille et al.  In order to attempt to make SED fitting more efficient, they have pre-calculated a large number of radiative transfer models that cover a reasonable amount of parameter space.  Then, for any given source, one can compare the observed SED to this set of models to quickly find the set of parameters that best explains the observations.

Let’s Get Technical

The online version of this fitting tool draws from 20,000 combinations of physical parameters and 10 viewing angles (if you are particularly curious, the online tool is available here).  A brief overview of the parameter space covered is as follows:

• Stellar mass between 0.1 and 50 solar masses
• Stellar ages between and years
• Stellar radii and temperatures (derived directly from stellar mass using evolutionary tracks)
• Disk parameters (disk mass, accretion rate, outer radius, inner radius, flaring power, and scale height) and envelope parameters (the envelope accretion rate, outer radius, inner radius, cavity opening angle, and cavity density) sampled randomly within ranges dictated by the age of the source

However, there are truly a vast number of parameters that could be varied in models of YSOs.  Thus, for simplicity, the authors are forced to make a number of assumptions.  Here are some of the biggest assumptions involved:

1. All stars form via accretion through a disk and an envelope.
2. The gas-to-dust ratio in the disk is 100.
3. The apparent size of the source is not larger than the given aperture.

The last constraint is not required, but it allows a number of model SEDs to be cut out and thus speeds up the process.  Furthermore, the authors make a point of saying that the results can always be scaled to account for varying gas-to-dust ratios, since only the dust is taken into account in the actual radiative transfer calculations.

Does This Method Really Work?

If this tool works well, it should be able to correctly reproduce previous results.  In order to test this out, the authors turn to the Taurus-Auriga star forming region.  They select a sample of 30 sources from Kenyon & Hartman (1995) that are spatially resolved, meaning that there is prior knowledge of their evolutionary stage from direct observations (i.e. there is a known result that astronomers are fairly certain of to compare the model fits against).  When fitting their model SEDs with the observed SEDs for this particular star forming region, the authors throw in a few additional assumptions:

1. All sources are within a distance range of 120 – 160 AU (helps to rule out models that are too faint or too luminous).
2. The foreground interstellar extinction is no more than = 20.
3. None of the sources appeared larger than the apertures used to measure fluxes.

The authors then assign an arbitrary cut-off in chi-squared for acceptable model fits: .  Here, is the of the best-fit model for each source.  Robitaille et al. acknowledge that this cut-off has no statistical justification: ‘Athough this cut-off is arbitrary, it provides a range of acceptable fits to the eye.’  After taking Jim Moran’s Noise and Data Analysis class, I for one would like to see the authors try a Monte Carlo Markov Chain (MCMC) analysis of their 14-dimensional space (for more detail on MCMC methods see this review by Persi Diaconis).  That might make the analysis a bit less ‘by eye’ and more ‘by statistics.’

The upshot of this study is that for the vast majority of the sources considered, the best-fit values obtained by this new SED fitting tool are close to the previously known values. Check.

It is also worth mentioning here, that there are many other sets of SED modeling codes.  One set of codes of particular note are those written by Paola D’Alessio (D’Alessio et al., 1998; D’Alessio et al., 1999; D’Alessio et al, 2001).  These codes were the most frequently used in the results presented at the ALMA conference I attended.  The distinct change in the D’Alessio models is that they solve for the detailed hydrostatic vertical disk structure in order to account for observations of ‘flared’ disks around T Tauri stars (flaring refers to an increase in disk thickness at larger radii).

But, Wait! There are Caveats!

Although the overall conclusion is that this method fits SEDs with reasonable accuracy, there are a number of caveats that are raised.  First of all, the models tend to overestimate the mid-IR fluxes for DM Tau and GM Aur (two sources known to have inner regions cleared of dust).  The authors explain that this is most likely due to the fact that their models for central holes assume that there is no dust remaining in the hole.  In reality, there is most likely a small amount of dust that remains.  Second, the models do not currently account for the possibility of young binary systems and circumbinary disks (relevant for CoKu Tau 1).

The paper also addresses estimating parameters such as stellar temperature, disk mass, and accretion rate from SED fits.  And, yes, you guessed it, these calculations raise several more issues.  For very young objects, it is difficult to disentangle the envelope and disk, making it very challenging to estimate a total disk mass.  To make these complications clearer, the set of two plots below from the paper show calculated values for the disk mass plotted against the accepted values from the literature.  It is easily seen that the disk masses for the embedded sources are the most dissimilar from the literature values.

Two plots from Robitaille et al. (2007) that show calculated values for the disk mass plotted against the accepted values from the literature. It is easily seen that the disk masses for the embedded sources (right) are the most dissimilar from the literature values.

Furthermore, even if the disk can be isolated, the dust mass in the disk is affected by the choice of dust opacity.  That’s a pretty big caveat!  A whole debate was started at the ALMA conference over exactly this issue and the authors have simply stated the problem and swept it under the rug in just one sentence.  In 2009, David Hogg conducted a survey of the rho Ophiucus region and used the models of Robitaille et al. (2007) to determine the best-fit dust opacity index, for this group of sources.   Hogg found that actually decreases for Class II protostars, a possible indication of the presence of larger grains in the disk.  Robitaille et al. also mention that the calculated accretion rates from SED fitting are systematically larger than what is presented in the literature.  The authors conclude that future models should include disk emission inside the dust destruction radius, the radius inside which it is too hot for dust to survive.  A great example of the complications that arise from a disk with a central hole can be seen in LkCa 15 (Espaillat et al., 2010; Andrews et al., 2011).   The figure below shows the observed and simulated SEDs for the source (left) as well as the millimeter image (right).  The double ansae (bright peaks or ‘handles‘ apparent on either side of the disk) seen in the millimeter contours are indicative of a disk with a central cavity.

Left: The observed and simulated SEDs for Lk Ca 15. The sharp peak seen at 10 microns is due to silicate grains within the inner hole of the disk. Right: The millimeter image of the disk. (Espaillat et al., 2010; Andrews et al., 2011)

In this case, a population of sub-micron sized dust within the hole is needed in order to produce the observed silicate feature at 10 microns.  Furthermore, an inner ring is required to produce the strong near-IR excess shortward of 10 microns.  A cartoon image of the predicted disk geometry is shown below.  To make things even more complicated, the flux at shorter wavelengths appears to vary inversely with the flux at longer wavelengths over time (Espaillat et al., 2010).  This phenomenon is explained by changing the height of the inner disk wall over time.

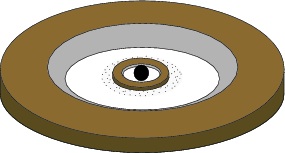
A cartoon image of the predicted disk geometry for Lk Ca 15 showing the outer ring, silicate grains within the hole, and the inner ring. (Espaillat et al., 2010)

Finally, Robitaille et al. discuss how well parameters are constrained given different combinations of data points for two example sources: AA Tau and IRAS 04361+2547.  In both sources, if only IRAC (Infrared Array Camera on the Spitzer Space Telescope) fluxes obtained between 3.6 and 8 microns are used, the stellar mass, stellar temperature, disk mass, disk accretion rate, and envelope accretion rate are all poorly constrained.  Things are particularly bad for AA Tau in this scenario, where only using IRAC data results in ~5% of all SED models meeting the imposed goodness of fit criterion (yikes!).  Adding in optical data to the mix helps to rule out models that have low central source temperatures and disk accretion rates.  Adding data at wavelengths longer than ~ 20 microns helps to constrain the evolutionary stage of the YSO, because that is where any infrared excess is most apparent.  And, adding submillimeter data helps to pin down the disk mass, since the emission at these longer wavelengths is dominated by the dust.  This just goes to show how necessary it is to obtain multi-wavelength data if we really want to understand YSOs, disks, and the like.

3. Sources:

Where to look if you want to read more about anything mentioned here…

• Andrews et al. (2011)
• D’Alessio et al. (1998)
• D’Alessio et al. (1999)
• D’Alessio et al. (2001)
• Dullemond & Monnier (2010)
• Espaillat et al. (2010)
• Hogg (2009)
• Isella (2006)
• Kenyon & Hartman (1995)
• Robitaille et al. (2007)

CHAPTER: Introductory Remarks on Radiative Processes

(updated for 2013)

The goal of the next several sections is to build an understanding of how photons are produced by, are absorbed by, and interact with the ISM. We consider a system in which one or more constituents are excited under certain physical conditions to produce photons, then the photons pass through other constituents under other conditions, before finally being observed (and thus affected by the limitations and biases of the observational conditions and instruments) on Earth. Local thermodynamic equilibrium is often used to describe the conditions, but this does not always hold. Remember that our overall goal is to turn observations of the ISM into physics, and vice-versa.

The following contribute to an observed Spectral Energy Distribution:

• gas: spontaneous emission, stimulated emission (e.g. masers), absorption, scattering processes involving photons + electrons or bound atoms/molecules
• dust: absorption; scattering (the sum of these two -> extinction); emission (blackbody modified by wavelength-dependent emissivity)
• other: synchrotron, brehmsstrahlung, etc.

The processes taking place in our “system” depend sensitively on the specific conditions of the ISM in question, but the following “rules of thumb” are worth remembering:

1. Very rarely is a system actually in a true equilibrium state.
2. Except in HII regions, transitions in the ISM are usually not electronic.
3. The terms Upper Level and Lower Level refer to any two quantum mechanical states of an atom or molecule where . We will use k to index the upper state, and j for the lower state.
4. Transitions can be induced by photons, cosmic rays, collisions with atoms and molecules, and interactions with free electrons.
5. Levels can refer to electronic, rotational, vibrational, spin, and magnetic states.
6. To understand radiative processes in the ISM, we will generally need to know the chemical composition, ambient radiation field, and velocity distribution of each ISM component. We will almost always have to make simplifying assumptions about these conditions.

CHAPTER: Measuring States in the ISM

(updated for 2013)

There are two primary observational diagnostics of the thermal, chemical, and ionization states in the ISM:

1. Spectral Energy Distribution (SED; broadband low-resolution)
2. Spectrum (narrowband, high-resolution)

SEDs

Very generally, if a source’s SED is blackbody-like, one can fit a Planck function to the SED and derive the temperature and column density (if one can assume LTE). If an SED is not blackbody-like, the emission is the sum of various processes, including:

• thermal emission (e.g. dust, CMB)
• synchrotron emission (power law spectrum)
• free-free emission (thermal for a thermal electron distribution)

Spectra

Quantum mechanics combined with chemistry can predict line strengths. Ratios of lines can be used to model “excitation”, i.e. what physical conditions (density, temperature, radiation field, ionization fraction, etc.) lead to the observed distribution of line strengths. Excitation is controlled by

• collisions between particles (LTE often assumed, but not always true)
• photons from the interstellar radiation field, nearby stars, shocks, CMB, chemistry, cosmic rays
• recombination/ionization/dissociation

Which of these processes matter where? In class (2011), we drew the following schematic.

A schematic of several structures in the ISM

Key

A: Dense molecular cloud with stars forming within

• (measured, e.g., from line ratios)
• gas is mostly molecular (low T, high n, self-shielding from UV photons, few shocks)
• not much photoionization due to high extinction (but could be complicated ionization structure due to patchy extinction)
• cosmic rays can penetrate, leading to fractional ionization: , where is the ion density (see Draine 16.5 for details). Measured values for (the electron-to-neutral ratio, which is presumed equal to the ionization fraction) are about .
• possible shocks due to impinging HII region – could raise T, n, ionization, and change chemistry globally
• shocks due to embedded young stars w/ outflows and winds -> local changes in T, n, ionization, chemistry
• time evolution? feedback from stars formed within?

B: Cluster of OB stars (an HII region ionized by their integrated radiation)

• 7000 < T < 10,000 K (from line ratios)
• gas primarily ionized due to photons beyond Lyman limit (E > 13.6 eV) produced by O stars
• elements other than H have different ionization energy, so will ionize more or less easily
• HII regions are often clumpy; this is observed as a deficit in the average value of  from continuum radiation over the entire region as compared to the value of n_e derived from line ratios. In other words, certain regions are denser (in ionized gas) than others.
• The above introduces the idea of a filling factor, defined as the ratio of filled volume to total volume (in this case the filled volume is that of ionized gas)
• dust is present in HII regions (as evidenced by observations of scattered light), though the smaller grains may be destroyed
• significant radio emission: free-free (bremsstrahlung), synchrotron, and recombination line (e.g. H76a)
• chemistry is highly dependent on n, T, flux, and time

C: Supernova remnant

• gas can be ionized in shocks by collisions (high velocities required to produce high energy collisions, high T)
• e.g. if v > 1000 km/s, T > 10⁶ K
• atom-electron collisions will ionize H, He; produce x-rays; produce highly ionized heavy elements
• gas can also be excited (e.g. vibrational H₂ emission) and dissociated by shocks

D: General diffuse ISM

• UV radiation from the interstellar radiation field produces ionization
• ne best measured from pulsar dispersion measure (DM), an observable.
• role of magnetic fields depends critically on X_I, n (B-fields do not directly affect neutrals, though their effects can be felt through ion-neutral collisions)